

Edit Distance
Get started
জয় শ্রী রাম
🕉Problem Statement:
In computer science, edit distance is a way of quantifying how dissimilar two strings (e.g., words) are to one another by counting the minimum number of operations required to transform one string into the other. There are three operations permitted on a word: replace, delete, insert. For example, the edit distance between "a" and "b" is 1, the edit distance between "abc" and "def" is 3.Given two words, develop an algorithm to compute their edit distance.
Solution:
Let dp[i][j] stands for the edit distance between two strings with length i and j, i.e., word1[0,...,i-1] and word2[0,...,j-1]. There is a relation between dp[i][j] and dp[i-1][j-1]. Let's say we transform from one string to another.The first string has length i and it's last character is "x"; the second string has length j and its last character is "y". The following diagram shows the relation.
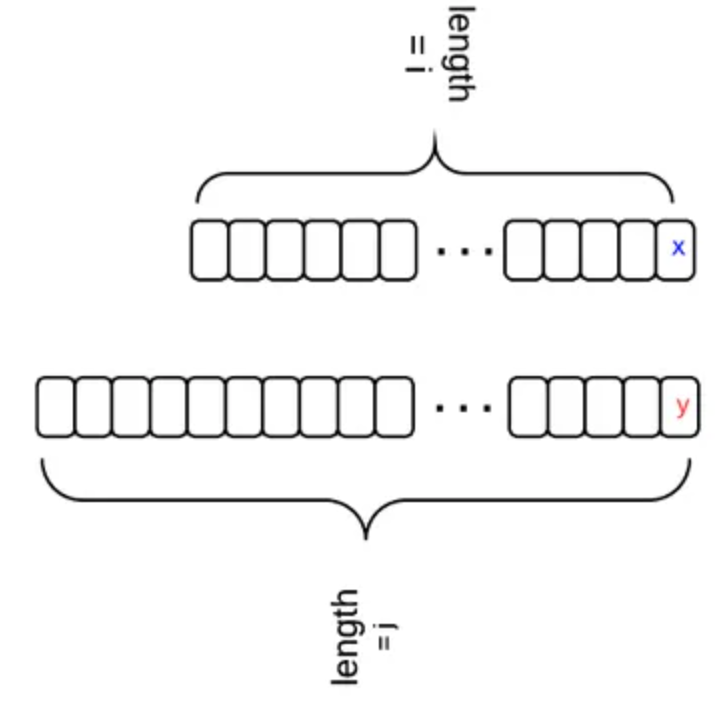
- if x == y, then dp[i][j] == dp[i-1][j-1]
- if x != y, and we insert y for word1, then dp[i][j] = dp[i][j-1] + 1
- if x != y, and we delete x for word1, then dp[i][j] = dp[i-1][j] + 1
- if x != y, and we replace x with y for word1, then dp[i][j] = dp[i-1][j-1] + 1
- When x!=y, dp[i][j] is the min of the three situations.
- Initial condition: dp[i][0] = i, dp[0][j] = j
Java Code:
Login to Access Content
Python Code:
Login to Access Content
