

Stock Trading With Transaction Fee
Get started
জয় শ্রী রাম
🕉Problem Statement:
Your are given an array of integers prices, for which the i-th element is the price of a given stock on day i; and a non-negative integer fee representing a transaction fee.
You may complete as many transactions as you like, but you need to pay the transaction fee every time you sell a stock. You may not buy more than 1 share of a stock at a time (ie. you must sell the stock share before you buy again.)
Return the maximum profit you can make.
Example 1:
Input: prices = [1, 3, 2, 8, 4, 9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
Buying at prices[0] = 1
Selling at prices[3] = 8
Buying at prices[4] = 4
Selling at prices[5] = 9
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
Solution:
- Finite state machines are a standard tool to model event-based control logic. If a given problem contains different events and depending on which event occurs we can transition from one state to another then it is highly likely that the problem could be solved using Dynamic Programming State Machine approach.
What differentiates a great problem solver from an average one is that the former has built a great ability in himself/herself to remove all the unnecessary data from a given problem statement and relate the given problem to a much simpler problem. Some problems, like this one, also contain some information which are important for computing the correct result, but not so important in coming up with the first iteration of an efficient algorithm. The introduction of transaction fee is an information that we definitely need to compute the correct result, but it is also playing one more role in this problem. It is making the problem look very convoluted (and diverting the problem solver to spend unnecessarily quite a bit of time on thinking on the transaction fee part) which is otherwise very very similar to a much simpler problem which is Compute Maximum Profit with Unlimited Stock Trade Transactions Allowed. Just that in current problem at hand, we have to take into account the transaction fee associated with every sale. There is no transaction fee for buying though.
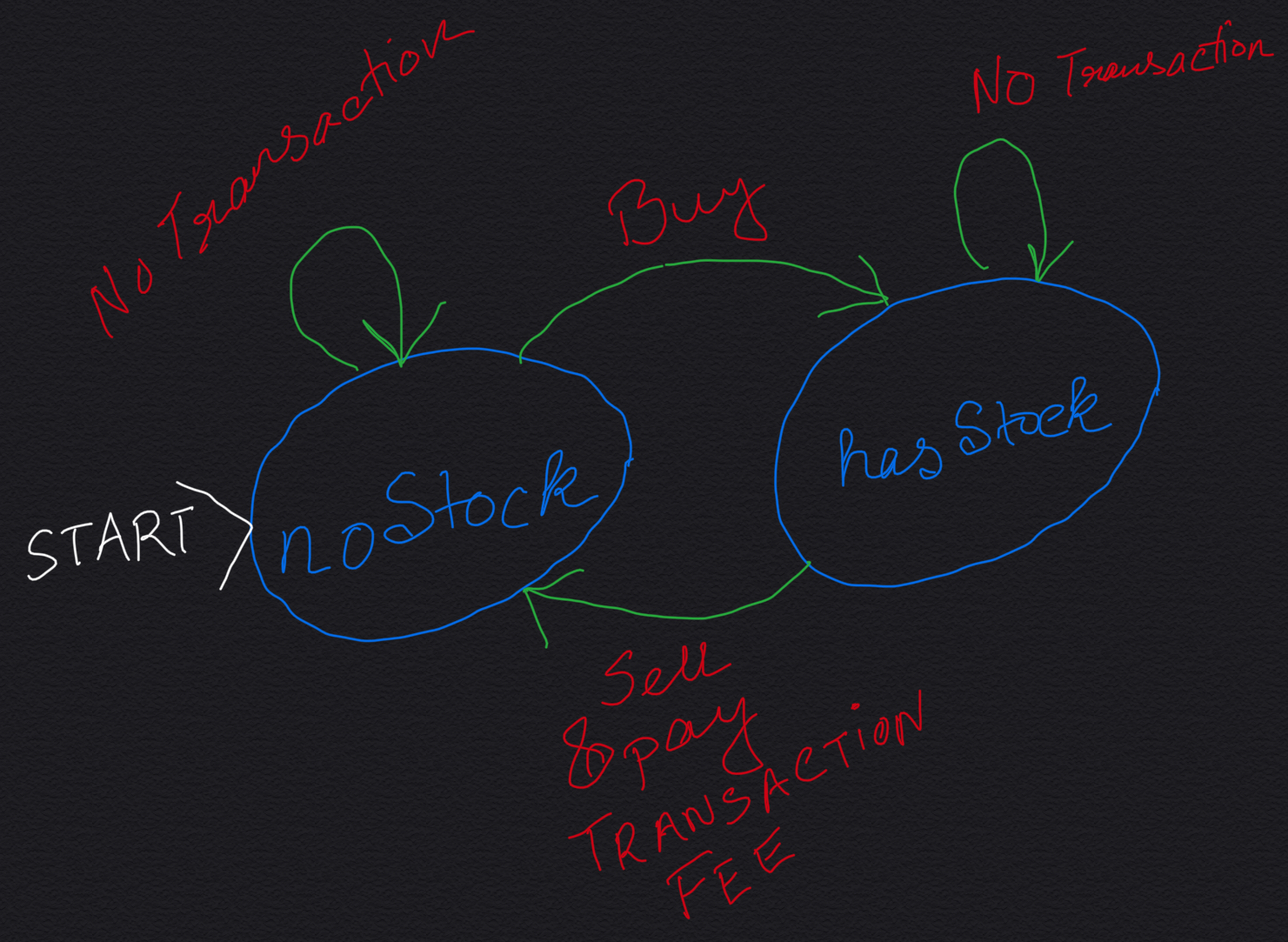
Every day we can be one of these two states:
- either we have a stock with us. Let's call this state hasStock state.
- or, we have no stock with us. Let's call this state noStock state.
Transition:
noStock state transitions to hasStock state by buying a stock.
hasStock state transitions to noStock state by selling the purchased stock and paying transaction fee.
noStock is also the START state, because on day-1 (first day) we start with a clean slate (no stock with us). Since we can make as many transactions as we want, this transitions can go on happening as many times as we want, keeping in mind that
- we cannot buy a stock before selling the one we already have with us.
- our goal is to maximize profit.
State Machine Diagram:
Recurrence Relation:
Let noStock[i] denote the maximum profit achievable at the end of day i if we have no stock with us on day i.
Let hasStock[i] denote the maximum profit achievable at the end of day i if we have a stock with us on day i.
We can transition to hasStock[i] in two ways:
- By doing nothing, i.e, transition from hasStock[i - 1].
-
From noStock[i - 1]: by buying one stock.
hasStock[i] = noStock[i - 1] - stockPrices[i]
We take the maximum of the above two, since our goal is to maximize profit:
hasStock[i] = Max(hasStock[i - 1], noStock[i - 1] - stockPrices[i])
noStock[i] can be reached by two ways:
-
From hasStock[i - 1] by selling stock and paying transaction fee.
noStock[i] = hasStock[i - 1] + stockPrices[i] - fee -
From noStock state of day before by doing nothing on day i.
noStock[i] = noStock[i - 1]
We take the maximum of the above 2 since our goal is to maximize profit:
noStock[i] = Max(noStock[i - 1], hasStock[i - 1] + stockPrices[i] - transactionFee)
This leads us to the following relations:
hasStock[i] = Max(hasStock[i - 1], noStock[i - 1] - stockPrices[i])
noStock[i] = Max(noStock[i - 1], hasStock[i - 1] + stockPrices[i] - transactionFee)
Return Value:
Since our goal is to maximize the profit we can never end the last day with a stock being held, because that would be waste of money that we bought a stock but did not sell it on or before the last day. So the return value would always be noStock[lastDay].
Base Conditions:
noStock[0] = 0
hasStock[0] = -stockPrices[0]
We get the above base cases using the below logic:
-
Ending the day with no stock being hold means we did not make any transaction.
We started the day with no stock and ended the day with no stock.
So net profit = 0;
noStock[0] = 0 -
If we end the first day with a stock being held that would mean that we started the day with 0 profit
and then spent stockPrices[0] to buy a stock where stockPrices[0] is the price of stock on the first day.
hasStock[0] = -stockPrices[0]
Java Code:
Login to Access Content
Python Code:
Login to Access Content
Space Optimization:
In the above code, we have room for Space Optimization because we do NOT need the hasStock[] and noStock[] arrays due to our below observation:
-
In the for loop notice that for every day = i we are relying on
hasStock[i - 1] and hasStock[i - 1].
At no point of time we are using anything more than that and so having the whole array in memory is adding no value when we are dependent on just these two values
So what we can do is we can take two variables that would hold the value of noStock[i - 1] and hasStock[i - 1] when we are processing for day = i.
We would also need two variables to hold noStock and hasStock values for the current day we are computing for.
The above discussion leads us to the below space optimized code:
Java Code:
Login to Access Content
Python Code:
Login to Access Content
The below code would walk you through how we can transform the non-space optimized code to space optimized one:
Java Code:
Login to Access Content
Python Code:
Login to Access Content
How would you Compute Optimal Path to maximize result, i.e, the days on which you would actually buy and sell stock(s) in order to maximize profit ?
Our goal now is to find out the days we would be purchasing stocks and the days we would be selling stocks that would maximize the overall profit.
In almost all the DP problems, finding the path that resulted in the optimal result takes little bit more thinking than just computing the optimal value.
It is always a good idea to first design the algorithm to compute the optimal value and then modify the code to find the optimal path. In most cases you would be reusing the logic you implemented to compute the optimal result, to compute the optimal path. We will see that in the below well-commented code.
Thought process involved in the solution:
- Using the same states we have been using so far,
it is very easily understandable from the State Machine Diagram that if we reach noStock state on day i from hasStock
state of day (i - 1), then that would mean that we sold a stock on day i.
But, a very important observation should be made here:
Let's say the stock prices for 5 days look like this : [1, 2, 3, 4, 5] , i.e, when the stock price soars. Starting from day-2 everyday we would think that today is the best day to sell since everyday we have better stock rate than day before. And starting from day-2 everyday we would transition to noStock state from hasStock (of day before). Try to convince this to yourself by working on this example. So, we cannot just go on adding a day to the sellingDay list just because we transitioned to noStock state from hasStock state. A very easy way to know when this scenario occurs is to see if all the already gotten purchase days and selling days are in pairs. Which means we would have more selling days in our list than the purchase days. But this is invalid since a selling day would always have a corresponding purchase day.The solution here is: if we see we are breaking the constraint that number of selling days cannot be more than total number of purchase days, we would know that this is the case where stock price is going up and we just got a better day to sell the last purchased stock. So remove the last stock selling day, and add the current day.
- If we transition to hasStock state from noStock on day i then day i is a purchase day. But if stock rate is declining like in [5, 4, 3, 2, 1] then everyday would prove to be a purchase day. In such scenario we need to remove the last purchase day and add the current as updated purchase day. It is very easy to detect such scenario: If we see that we already have more purchase days than selling days we would know that we are in a situation when stock prices is declining giving us better day for stock purchase.
Java Code:
Login to Access Content
Python Code:
Login to Access Content
Don't forget to look at the other problems in our State Machine Approach series to have a strong understanding and a good command of this concept:
- Stock Trading With Cooldown
- Max Profit w/ at most 2 Stock Trade Transactions
- Max Profit w/ at most K Stock Trade Transactions
- Max Profit w/ Unlimited Stock Trade Transactions
- Max Profit w/ at most 1 Stock Trade Transaction
