

Kruskal's Algorithm and Minimum Spanning Tree
Get started
জয় শ্রী রাম
🕉Minimum Spanning Tree:
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight.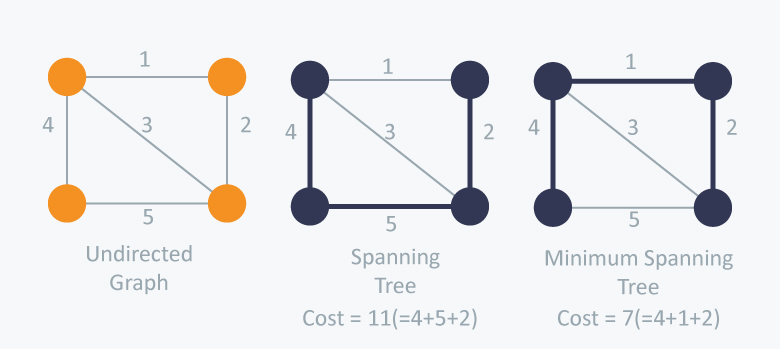
Kruskal's Algorithm
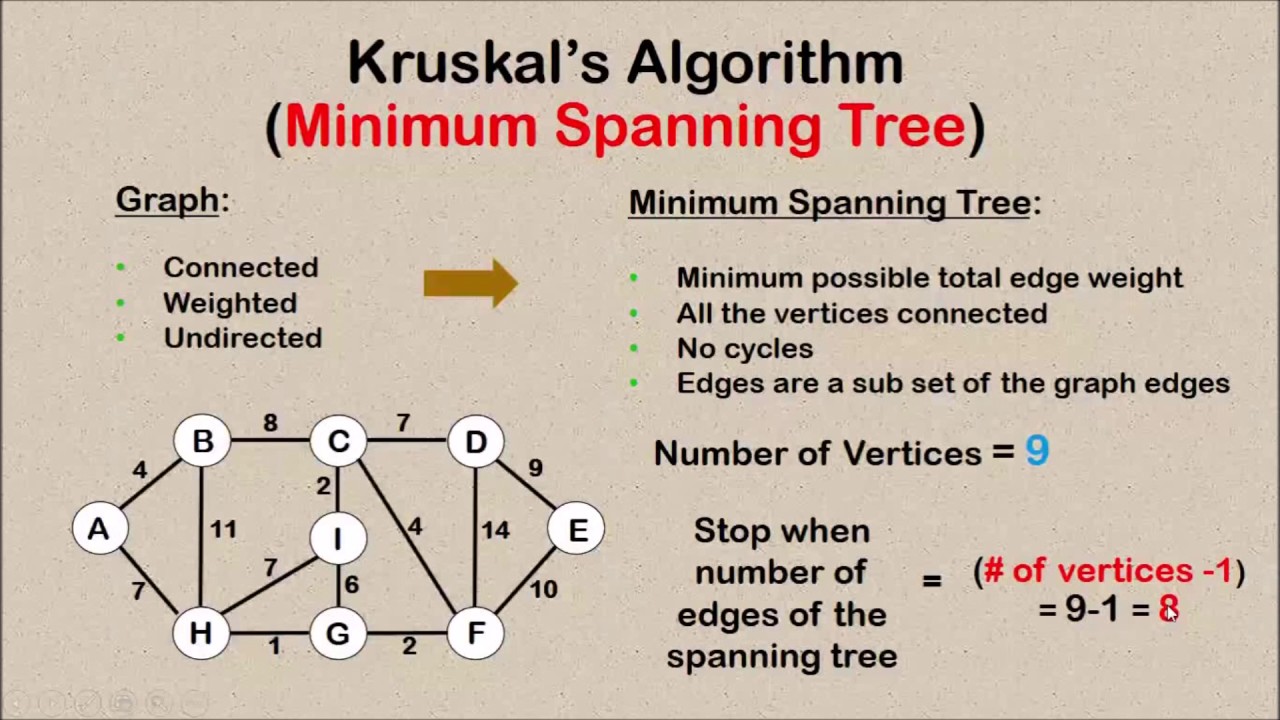
-
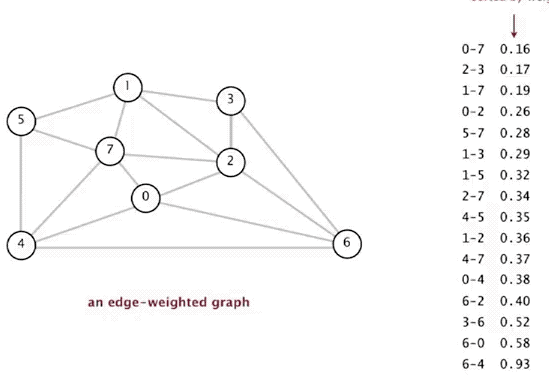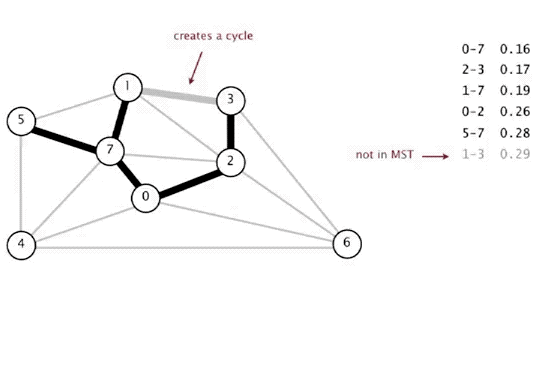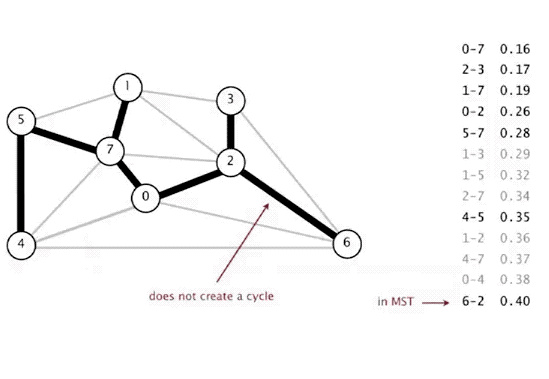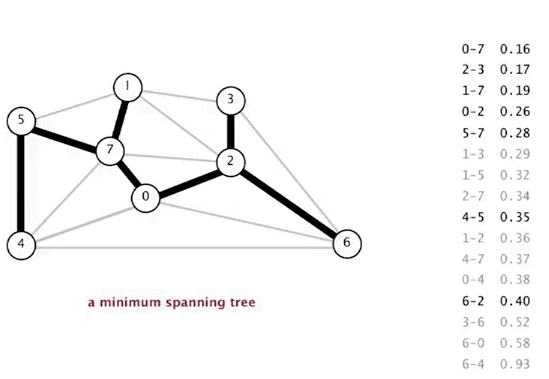
Sort all the edges in non-decreasing order of their weight.
-
Pick the smallest edge.
Check if it forms a cycle with the spanning tree formed so far.
If cycle is not formed, include this edge. Else, discard it.
It is very important to understand why we are avoiding cycle in the minimum spanning tree. Let's take a very simple example: let's say in edges AB and AC are included in the partial minimum spanning we have found till now. Let's say the given graph also have an edge BC. Now if we have already added AB and AC in the partial spanning tree,that would mean that BC has higher weight than that of AC and AB. Now adding BC will not any value to us since it is not connecting the partial spanning tree to any new vertex as B and C are already part of the spanning tree using edges with lower weight than that of BC.
Now, what is an efficient way to detect cycle? If you have read 4 Ways to Finding Cycles you know that we can use Union-Find to detect cycle very easily and efficiently using Weighted Union-Find and Path Compression.
- Repeat step#2 until all vertices are included in the spanning tree. If there are V vertices in the given graph, the there will be (V - 1) edges in the minimum spanning tree.
We will learn implementation of Kruskal's Algorithm by solving a real world problem.
Problem Statement:
You have been hired as a chief architect by an real estate developer to build a new housing community. You need to supply water to all the houses in the community by building wells and laying pipes. For each house you can either build a well inside it directly or bring water from another well to it using pipes. You know the cost of building well inside each house. You also know the cost of laying pipes between houses to bring water from a well located in a different house.
Connections are bidirectional, and there could be multiple valid connections between the same two houses with different costs. Also there could be pairs of houses for which there could be no direct pipes between them.
Compute the minimum total cost to supply water to all houses.
Solution: This is a very interesting problem that has been asked multiple times at Google in past.
This problem may at first seem like a very hard and convoluted problem, but we will see how knowing Kruskal's Algorithm will help us come up with a super simple yet super elegant and efficient solution.
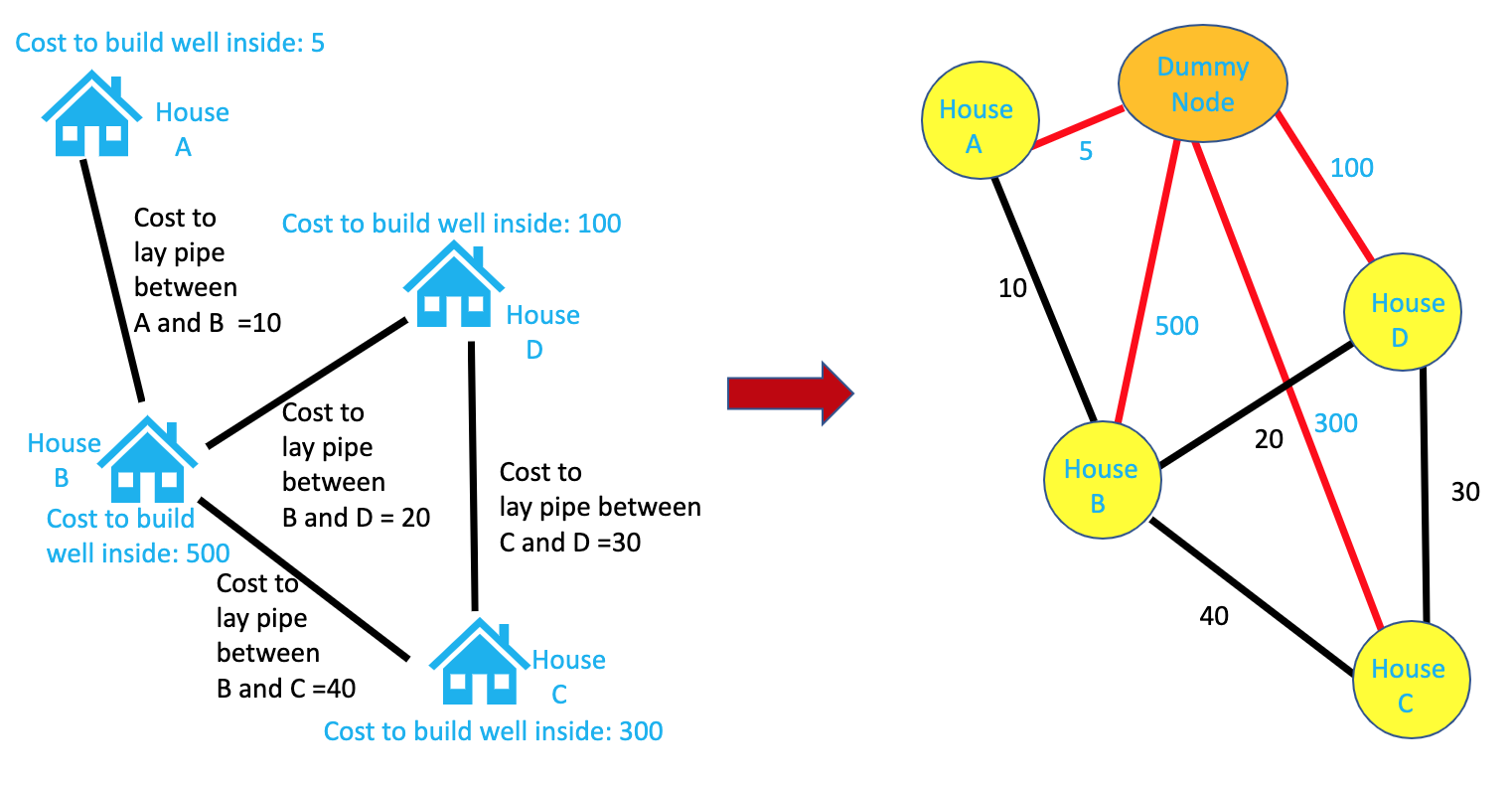
In the above problem, we know the cost to build a well inside each house. We also the cost for piping water in between any two house.
We can think of houses as vertices and represent the water connection between them. The weight of the edges will denote the cost to laying pipes between the two nodes. So, graph will be a perfect data structure to represent the whole housing community network. But how do we denote the cost of the constructing well inside a house ? It is not very common to have weights for vertices and doing so will only add complexities. Instead we will do something different. We will add a dummy node and have edge from this dummy node to all other nodes and the edge weights will represent the cost of constructing well in the nodes (houses). This is a very POWERFUL technique which will often come handy in simplifying some complex graph problems.
After reading the problem statement, the problem may look like a shortest path problem since it asks us to calculate the minimum total cost. So you might be thinking of using Dijkstra's Algorithm. But once you start thinking deeper, you realize trying to use Dijkstra's Shortest Path Algorithm only makes it complicated and does not lead to a solution. Dijkstra's algorithm will require us to treating the dummy node as the source (since we would need to construct well in at least one house) and then computing shortest path from the source to all other nodes (houses). But this would not give you the overall minimum cost to supply water to all houses. Why? Look at below graph:
5
A--B
2 / /3 \ 3
Dummy----- C
9
Cost to construct wells in house A, B and C are 2, 3 and 9 respectively. And laying pipes between A and B costs 5, between B and C costs 3. Cost to lay pipes between other houses (example: A to C)are not mentioned, so can be assumed INFINITY.
Dijkstra will give shortest path between Dummy to C as direct connection with cost 9. Even for vertices A and B the shortest paths will be direct connection, resulting in total of (9 + 2 + 3) = 14 as total cost to supply water to all houses. But for us to supply water to all houses in the least expensive way, we should connect Dummy to A to B to C resulting in total cost as (2 + 5 + 3) = 10.
So, Dijkstra's Algorithm is off the table to solve this problem. But the above thought process gave us a deeper insight on what we are actually trying to compute. We are actually trying to compute a minimum spanning tree of the above graph in order to get the minimum cost to supply water to all houses.
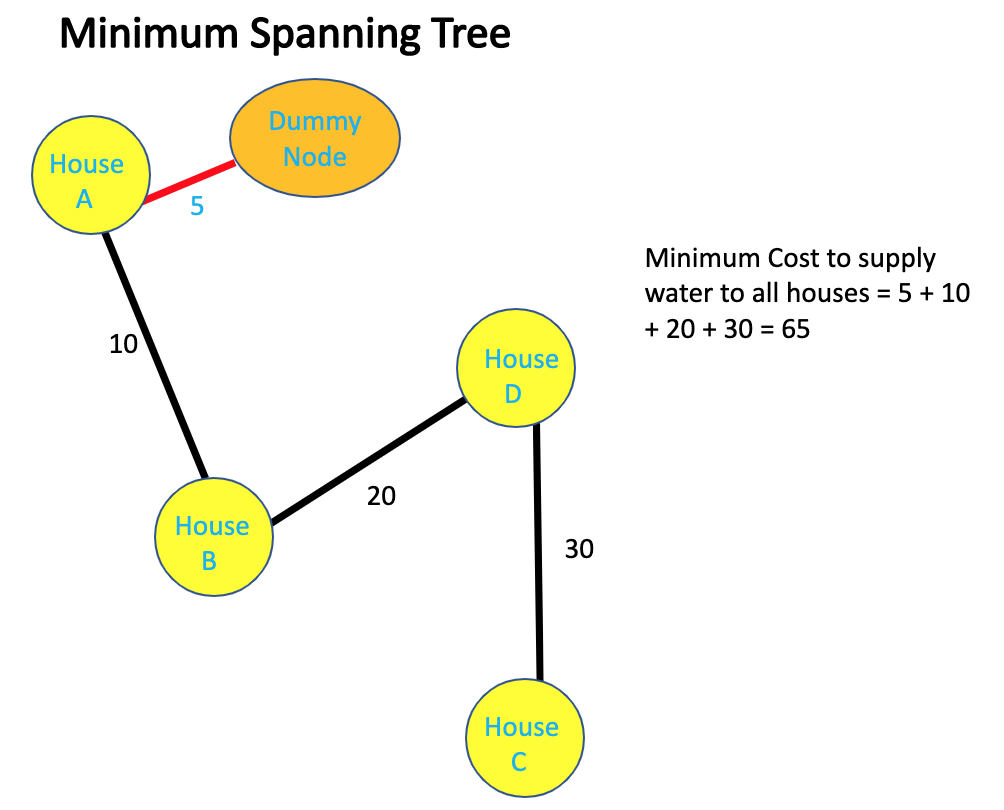
Now that we have a solution, let's see how implement computing spanning tree using Kruskal's algorithm.
Java:
class HousingCommunity {
// n = total number of houses. Houses are numbered from 1 to n
// wells[i - 1] = cost to build a well inside house i. Length of wells[] array = n, indexed from 0 to (n - 1)
// pipes[] array contains costs to lay pipes between houses. pipes[j] = [house1, house2, cost] represents the cost to connect house1j and house2j together using a pipe
public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
List<Integer> housesWithWells = new ArrayList<>(); // this list will contain all the houses inside which wells will be contructed to supply water to entire housing community with minimum cost
/* BEGIN - build graph */
List<int[]> edges = new ArrayList<>();
for (int[] pipe : pipes) {
edges.add(pipe);
}
// now add the dummy node and its connection to all the houses.
// lets denote dummy node as 0
// since the existing houses are numbered from 1 to n
for (int i = 0; i < wells.length; i++) {
edges.add(new int[] {0, i + 1, wells[i]});
}
/* END - build graph*/
// now sort the edges since we will be using Kruskal's Algorithm
Collections.sort(edges, (a, b) -> a[2] - b[2]);
UnionFind uf = new UnionFind(n + 1); // (n + 1) since we have one dummy node
int cost = 0;
for (int[] sortedEdge : edges) {
if (uf.find(sortedEdge[0]) != uf.find(sortedEdge[1])) { // check if we are getting a cycle
// not forming a cycle, so lets do our required processing
uf.union(sortedEdge[0], sortedEdge[1]); // since this edge is not forming a cycle,
// include this edge in our minimum spanning tree
cost += sortedEdge[2];
if (sortedEdge[0] == 0) {
// if this house is connected to dummy node and
// is becoming part of our minimum spanning tree
// that would mean that we are building a well inside this house
housesWithWells.add(sortedEdge[1]);
}
}
}
for (int houseWithWell : housesWithWells) {
System.out.print(houseWithWell + " ");
}
return cost;
}
public class UnionFind {
int[] root; // root[i] = root of the component to which node i belongs
int[] size; // size[i] = size of a component with root as i
public UnionFind(int n) {
root = new int[n];
size = new int[n];
for (int i = 0; i < n; i++) {
root[i] = i;
size[i] = 1;
}
}
public int find(int node) {
// perform path compresion
if (root[node] != node) {
root[node] = find(root[node]);
}
return root[node];
}
public void union(int node1, int node2) {
int root1 = find(node1);
int root2 = find(node2);
if (root1 == root2) {
return;
}
if (size[root1] > size[root2]) {
size[root1] += size[root2];
root[root2] = root1;
} else {
size[root2] += size[root1];
root[root1] = root2;
}
}
}
}
Python:
class UnionFind:
def __init__(self, n):
self.root = []
self.size = []
self.root = [0 for _ in range(n)]
self.size = [0 for _ in range(n)]
for i in range(0, n):
self.root[i] = i
self.size[i] = 1
def find(self, node):
# perform path compresion
if self.root[node] != node:
self.root[node] = self.find(self.root[node])
return self.root[node]
def union(self, node1, node2):
root1 = self.find(node1)
root2 = self.find(node2)
if root1 == root2:
return
if self.size[root1] > self.size[root2]:
self.size[root1] += self.size[root2]
self.root[root2] = root1
else:
self.size[root2] += self.size[root1]
self.root[root1] = root2
-----------------
class HousingCommunity:
def minCostToSupplyWater(self, n, wells, pipes, uf=None):
housesWithWells = []
# BEGIN - build graph
edges = []
for pipe in pipes:
edges.append(pipe)
i = 0
while i < len(wells):
edges.append([0, i + 1, wells[i]])
i += 1
# END - build graph
cost = 0
for sortedEdge in edges:
if uf.find(sortedEdge[0]) != uf.find(sortedEdge[1]):
cost += sortedEdge[2]
if sortedEdge[0] == 0:
housesWithWells.append(sortedEdge[1])
for houseWithWell in housesWithWells:
print(str(houseWithWell) + " ", end = '')
return cost
So, to summarize, figuring out that we would have to add a dummy node was the only hard part. Once we figured that out, the problem boiled down to just finding a minimum spanning tre.
