

Parallel Jobs Scheduling Problem with Precedence
Get started
জয় শ্রী রাম
🕉
Prerequisites:
Longest Paths Algorithm,
Sequential Job Scheduling
Parallel Jobs Scheduling Problem with Precedence type of job scheduling problems are very similar to Sequential Job Scheduling except that in this case you can execute more than one job at the same time if they are eligible to be executed parallelly. A job is eligible to be executed only when all the jobs it is dependent on have been completed/executed. Also in this case, each job is generally accompanied by a specified duration it takes to complete. These durations would play a critical role in designing a solution.
Problem Statement: Given a set of jobs of specified duration to be completed, with precedence constraints that specify that certain jobs have to be completed before certain other jobs are begun, how can we schedule the jobs on identical processors (as many as needed) parallelly such that they are all completed in the minimum time possible while still respecting the constraints ?
Let's say we are given the below jobs that we need to complete
Job id Duration Must complete after the completion of jobs # ------ -------- -------------------------------------------- 0 2 1 4 2 2 0 3 6 0 , 1 4 2 5 4 2 , 3, 4
So we have the following dependencies here :
- 0 -> 2 and 0 -> 3, i.e, job 0 must complete before job 2 and 3,
- 1 -> 3, i.e, job 1 must complete before job 3
- 2 -> 5, i.e, job 2 must complete before job 5
- 3 -> 5, i.e, job 3 must complete before job 5
- 4 -> 5, i.e, job 4 must complete before job 5
_ 2 -------
/| \
/ \
/ _\|
0 ----> 3 -----> 5
^ ^
| |
| |
1 4
We can also show the duration of the jobs in the graph. If say job V and W can start only after job U has completed, and duration of job U is d, then the weight of the edges UW and UV would be the duration of job U i.e, d. The edge weight would indicate that job W and job U are at least d time duration apart. Same goes for jobs V and U.
So, now let's modify the graph accordingly to include durations:
_ 2 ---(2)------
/| \
/(2) \
/ _\|
0 --(2)--> 3 --(6)---> 5
^ ^
| (4) | (2)
| |
1 4
So, let's see what's going on here:
Our objective is to finish up all the jobs in as less time as possible. We can achieve this by scheduling every job at its earliest. Since we have as many processors as needed available and can process the jobs parallelly, even if more than one jobs demand to be processed at the same time, we can. The more dependency a job has on other jobs, the more cautious we need to be about scheduling the job to make sure all the jobs it is dependent on have completed before it is scheduled. So let's pick up the one which has the most dependency, for our case it is job 5. Job no. 5 cannot start until job 2, 3 and 4 have completed. So whichever of these 3 jobs (job 2, 3 and 4) would have the latest completion time, would dictate the earliest start time of job 5. From our graph we see that it is job 3 that decides the earliest start time of job 5. Because job 2 ends at time 4, job 3 ends at time 8 and job 4 ends at time 2, at the earliest. So even if job 2 and 4 end earlier than job 3, job 4 would still have to wait for job 3 to complete.
Now let's see what's going on with job 3. We see job also has the same constraint. Job 3 will have to wait for whichever of job 0 and job 1 completes later than the other.
We can say the same thing for all the vertices (jobs) in the graph.
Algorithm:
-
So, what we see here in the graph is that for every vertex, we need to reach them through the longest path from the source vertex for that path.
So what this means is: to find the minimum time by which we would be able to complete all jobs we need to find longest distance
from all the source to all other vertices and then pick the longest of them all.
Very important to note, while computing
the weights of the paths, don't forget to add the duration of the last job in the path. An easy to do is add one extra vertex. Let's
call this vertex terminal vertex.
Create a directed edge from all vertices to the terminal vertex. The edge weight of each of these edges would be
the duration of the job vertex from which it originated. The graph below illustrates this.
So now with this extra terminal node, we
would have a little modification in our algorithm Instead of computing longest path from every node to every other node, we can just compute
longest path from every node to terminal vertex.
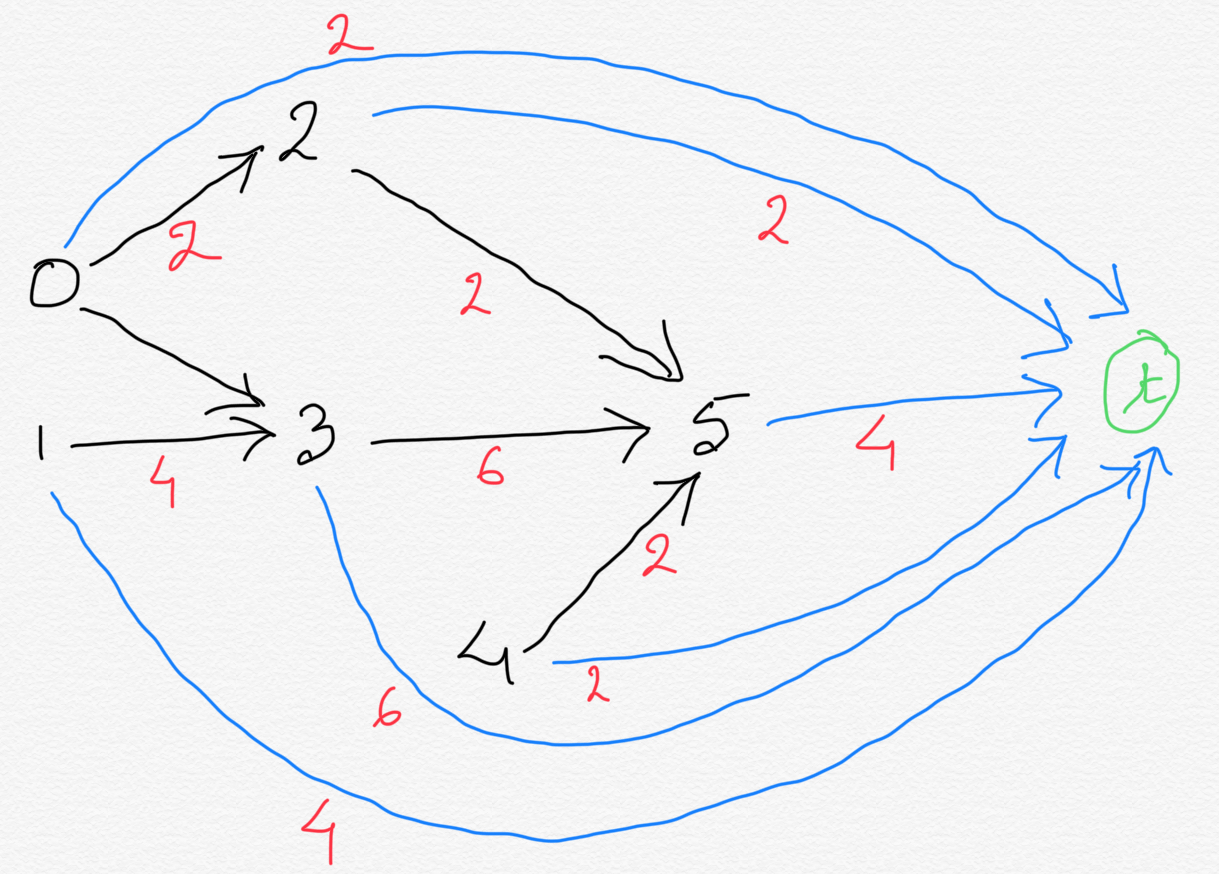
-
We can further optimize it. Notice how we do NOT need the edges to terminal vertex from the vertices
which already had at least one outbound edges. What this means is, for any job on which other jobs are dependent, we do not need
an extra edge to the terminal vertex. Adding the extra edge would add no value, since other jobs are dependent on this job,
this job cannot end an execution path. There will be at least one more job that needs to be done after this job complete.
This is true for all the jobs except job 5.
In general, we should have an edge to the terminal vertex only
from those vertices which had no outbound edges.
So now our graph now looks like this:
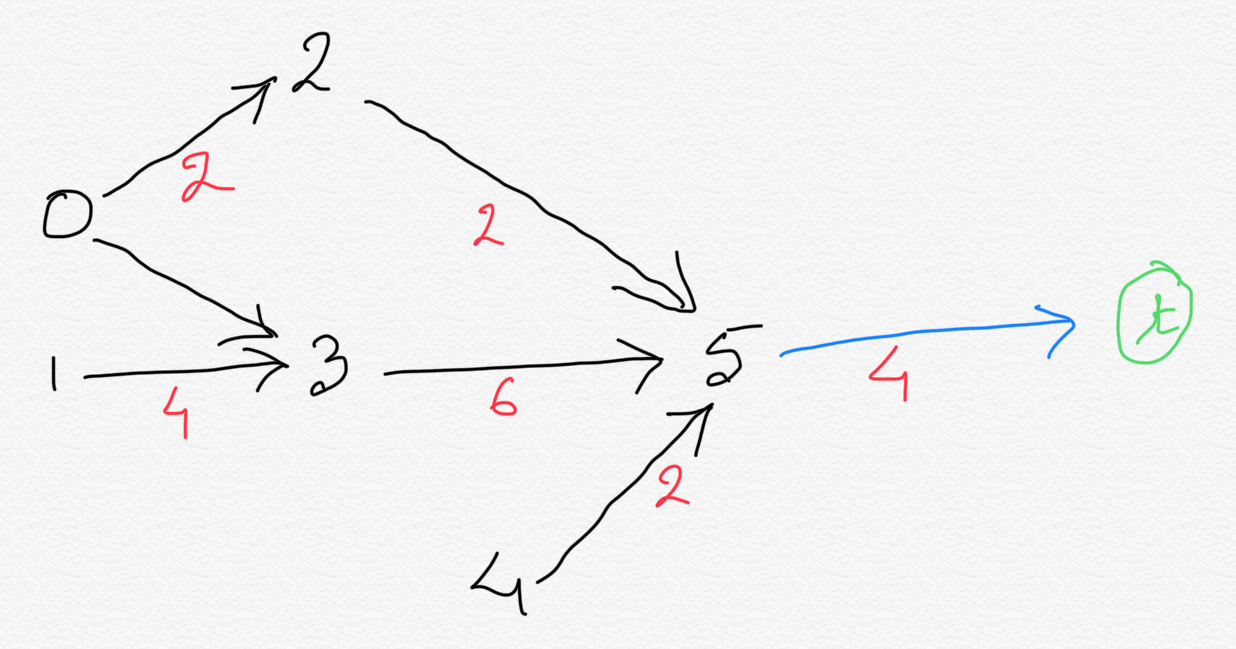
-
There is still room for optimization. There is no need compute longest path from every vertex. Instead just like how we added terminal vertex
and connected that to the vertices with no outbound edges. We can apply similar concept on the vertices with no inbound edges.
Let's add an extra vertex called source vertex and add directed edge from source vertex to all the vertices with
zero inbound edges. The weight of these edges we added would be ZERO, since source vertex is a dummy job.
So now, all we need to do is compute longest path from source vertex to terminal vertex.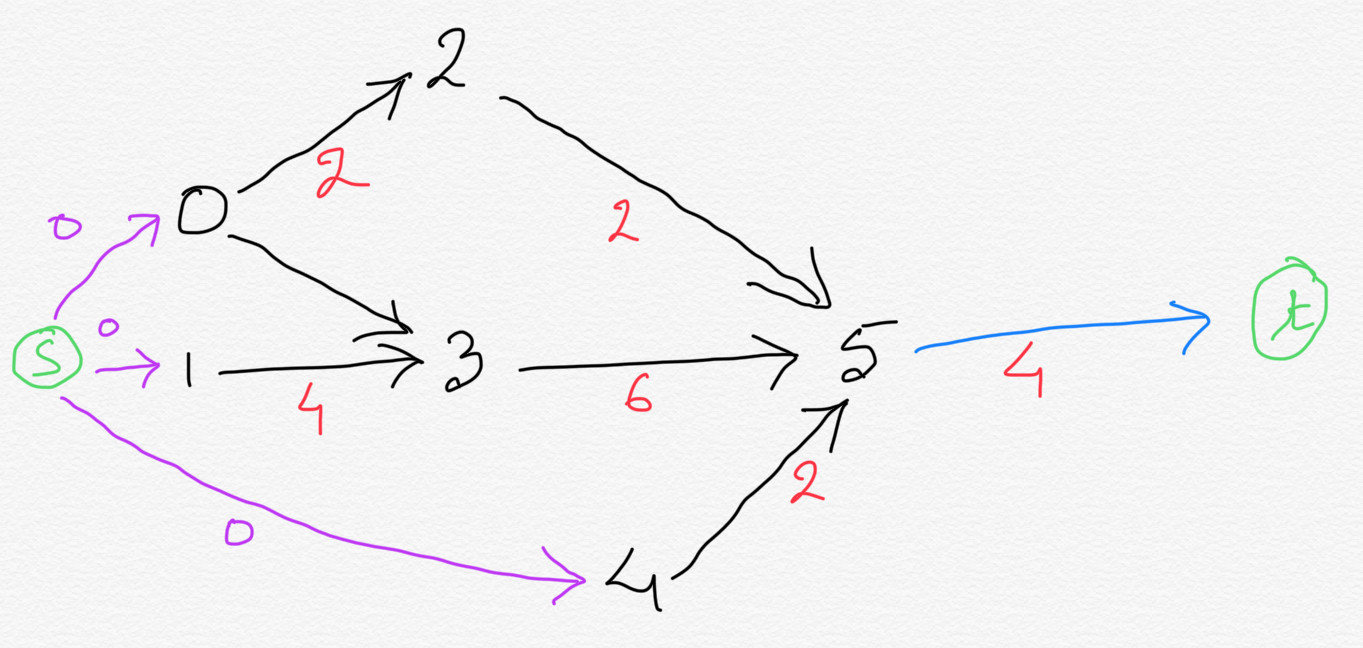
If we have to schedule all the jobs at the their earliest time then only the below will be valid:
Processor 1: < --Job0-- > < -----------Job3-----------> < ----Job 5---- > (critical path) Processor 2: < --Job2-- > Processor 3: < --Job4-- > Processor 4: < ----Job1---- > Time: 0 2 4 8 10 12
The algorithm discussed here will give you the above configuration. In fact after running the below our algorithm (code below), distance[i] will give the earliest scheduling time for all the jobs.
We are computing longest path to every job, which basically gives you the earliest time when you can start a job while maintaining all the constraints. distance[i] gives the longest distance of vertex i from the source vertex.
But, if our objective is to get the jobs done in minimum time, as well as use as less processors as well then we would have something like below (all those that use only two processors):
Processor 1: < --Job0-- > < -----------Job3-----------> < ----Job 5---- > Processor 2: < --Job2-- > < ----Job1---- > < --Job4-- > Time: 0 2 4 8 10 12 OR, Processor 1: < --Job0-- > < -----------Job3-----------> < ----Job 5---- > Processor 2: < ----Job1---- > < --Job4-- > < --Job2-- > Time: 0 2 4 8 10 12 OR, Processor 1: < --Job0-- > < -----------Job3-----------> < ----Job 5---- > Processor 2: < --Job4-- > < ----Job1---- > < --Job2-- > Time: 0 2 4 8 10 12
Notice how Job 1 and Job 4, since they have no dependency on any other jobs, can be scheduled anytime as long as they are completed before the completion of the longest path. The same is not true for Job 0 though, even though it has no dependency on any other jobs. It is because job 0 is part of the longest path that determines the overall minimum time that would spent in executing all jobs maintaining all constraints. For our case this longest path is 0 -> 3 -> 5. The total time duration of this longest path dictates the overall time taken to complete all the jobs. This longest path is called critical path. Any delay in this critical path would delay the overall processing time. Since we can use as many processors as we want, any jobs not part of the critical path can be processed with more leeway as long as their completion time is not later than the completion time of the critical path.
Code Implementation:
Please subscribe to access the complete working solution.
After subscribing please come back and refresh this page.
Time Complexity:
Same as Longest Paths Algorithm: O(E + V). In worst case it is O(V2) for a dense graph where most jobs has most other jobs as their DIRECT/IMMEDIATE dependencies.Note:
-
In the above implementation, distance[i] gives the EARLIEST possible start time for job i, for all i >= 0 and i < n.
Remember what we are doing here. We are computing longest path to every job, which basically gives you the earliest time when you can start a job while maintaining all the constraints.
distance[i] gives the longest distance of vertex i from the source vertex. -
longestPaths.getLongestPath(n)gives the critical path, where n is the terminal vertex id.
Related Must-Read Topics:
- Dijkstra's Algorithm
- Longest Paths Algorithm
- Topological Sort w/ Vertex Relaxation
- Bellman-Ford Algorithm & Negative Cycle Detection
- Optimized Bellman-Ford
- Sequential Job Scheduling
-
Parallel Job Scheduling
w/ Relative Deadlines - Arbitrage
