

Closest Pair of Points
Get started
জয় শ্রী রাম
🕉
Prerequisite: Fundamentals of Sweep Line Algorithm
In this chapter we will try to find the closest pair of points among a given set of points in X-Y plane using Sweep Line Technique and efficient O(logn + R) Range Search query.
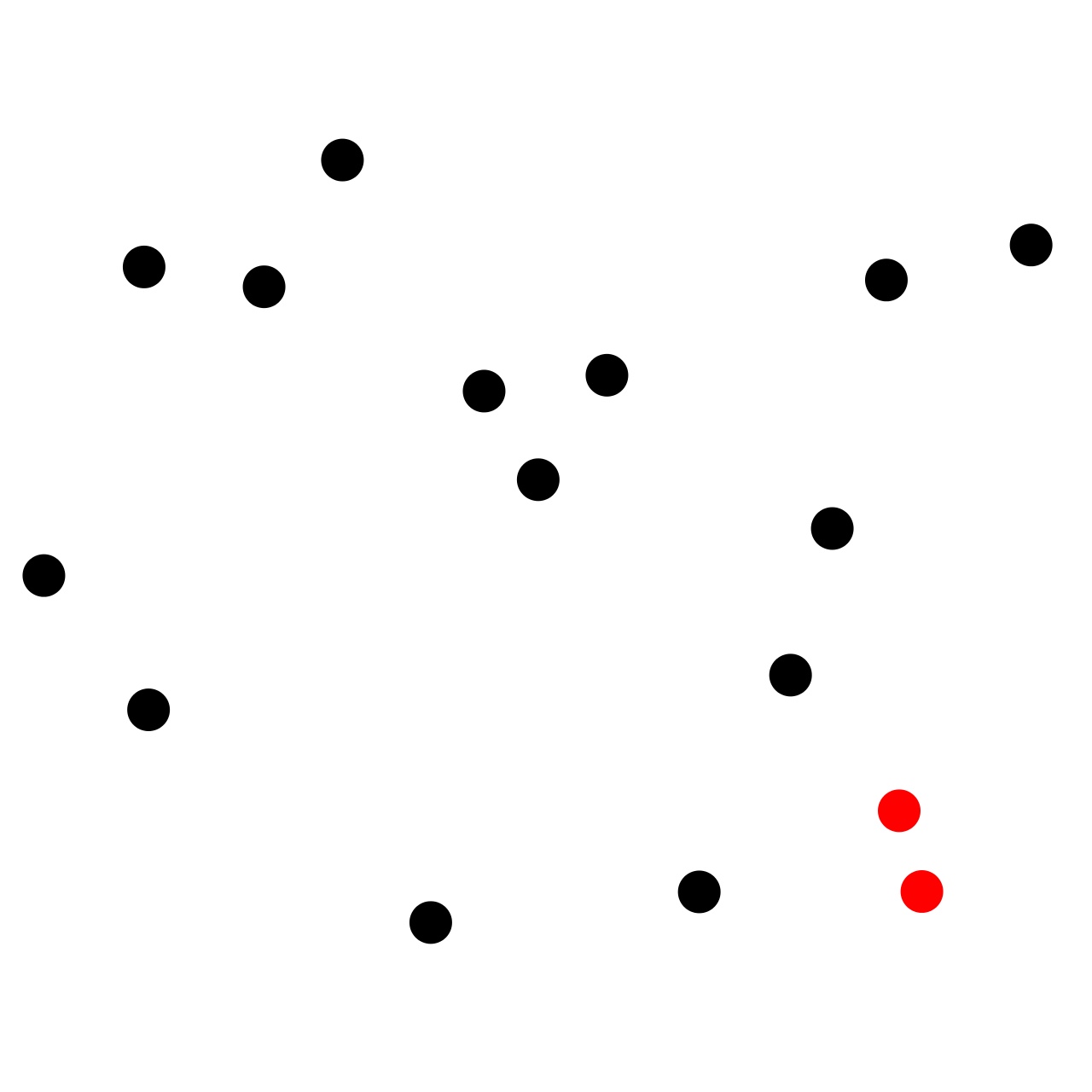
The closest pair of points problem or closest pair problem is a problem of computational geometry: given n points in metric space, find a pair of points with the smallest distance between them.
In the diagram below, the pair of points in red is the closest pair among all the pairs present.
Algorithm:
Many think this problem as a moderate or slightly hard, but it is not if you think of it in generalized way. Just think, if you sweep a vertical line across the plane treating all the given points as events and scan the points (events) one by one from left to right and process them then how would you process the current point at hand based on the points already processed (i.e.,already processed events). Here, processing means computing distances between current point and its nearby points and computing if the current point's distance from any of its neighboring point happens to be the closest or minimum distance till now. Do we need to compute the distance between the current event (point) we are processing with all the events (points) on its left ? The answer is NO. If we compute distance with all the points on the left of the current point, that would be a waste of time, because we can do better than that. Say, we have an array of n points points[0...n-1] and lets say the current point we are processing is points[k]. If we already know that d1 is the minimum distance between two points we have found till now, will we gain anything by computing the distance between the current point with the points on left which we know are more than the distance from the current point points[k]? No, we won't. So, we will be computing distance from current point to only those already processed points/events which are less than d1 distance.How can we achieve this? We know, two points for which the difference between their x-coordinate is greater than or equal to d1 then the two points are at least d1 distance apart. Same goes for the y-coordinates of the two points. If the difference between their y-coordinates is greater than or equal to d1 then the two points are at least d1 distance apart from each other.
So, what we would do is: sort given set of points in ascending order of their x-coordinate. For every point/event we process, we keep track of the index of the point that was d1 distance away from the current point under process, where d1 = minimum distance found till the previous point/event processed. So now we have all the points which are within d1 x-distance away from the current point. Now that we have come this far, let's narrow it down even further. Among all these points we have got (which are within d1 x-distance away fro the current point) the points which are more than d1 y-distance away from the current point is of no interest to us for the current point under process.
So we should narrow down the points of interest by removing the points which are more than d1 y-distance away from the point under process. Then we compute distance between point under process and all of those narrowed down points. We can use range search to achieve this. We will soon see that the maximum number of points that can be present in this narrowed down group is 5.
We do the above described process for all the points in a given set to get the overall closest pair and the overall minimum distance. We initialize d1 with positive infinity and go on updating d1 with the minimum distance found at each iteration.
Why do we compute distance of the current point from the points on left and not on right ?Or, why does the active events have points only from the left of the current point and not from the right of it ?
Because we would be processing the points on the right anyway (as we iterate from left to right), so no use of processing them twice.While processing a point, after we have gotten points on left which are less than d1 x-distance and d1 y-distance away from the current point, how many points there can be be in this group of points/events of interest ? d1 = minimum distance between two points found till processing the previous point
Let's look at the diagram below. Let's suppose d1 is the minimum distance between two points found till now, and the point around which we have the rectangle drawn is the current point. We can clearly see from the diagram that in the drawn rectangle we can have at most 5 points around the current point because if we have more than 5 points there would be at least three pairs of points which are less than d1 distance away and that is not possible because d1 is the minimum distance till now, and if there were distance less than d1 (say d2) then we would have d2 as the minimum distance till now, not d1.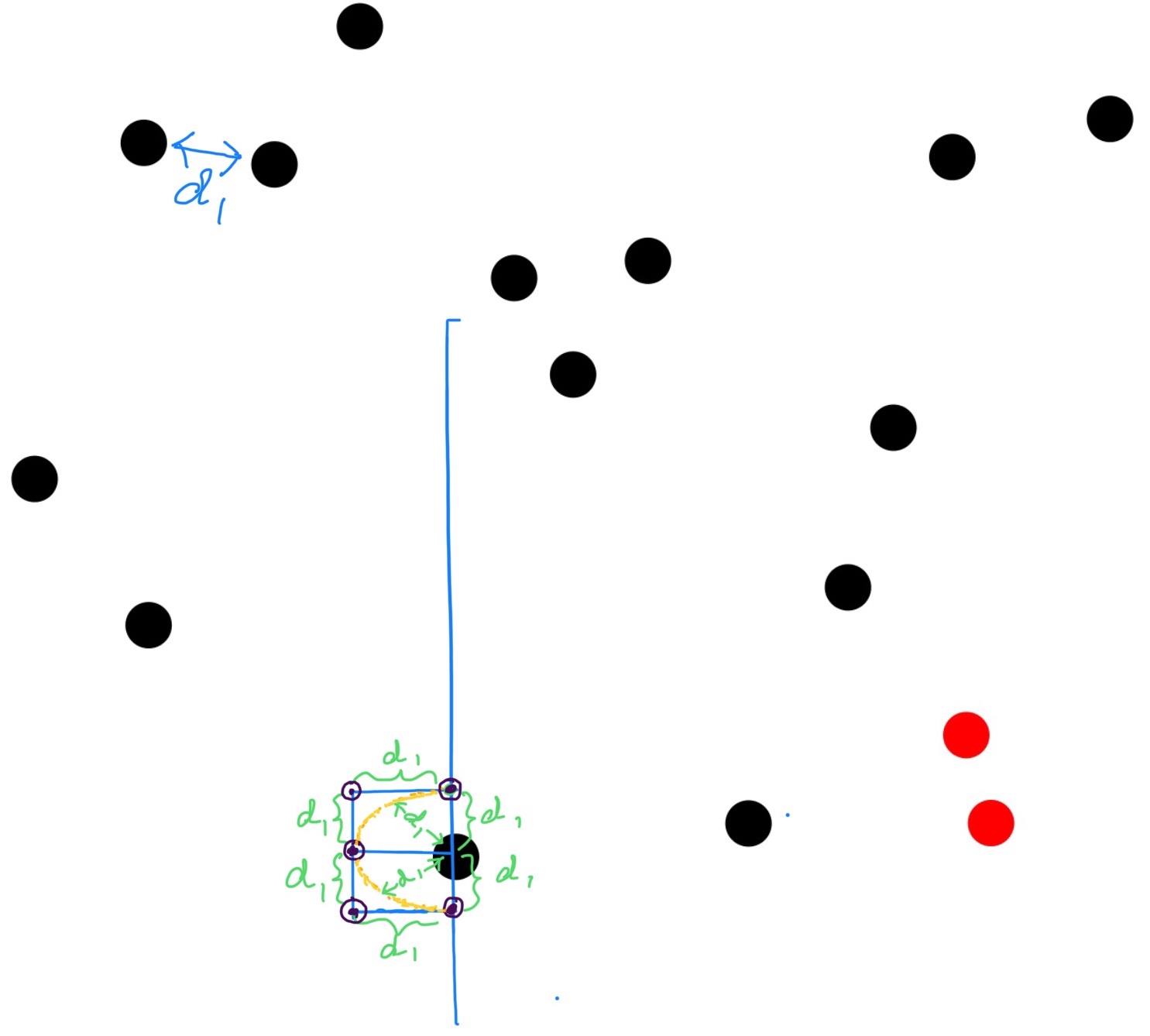
How do we compute distance between two points ?
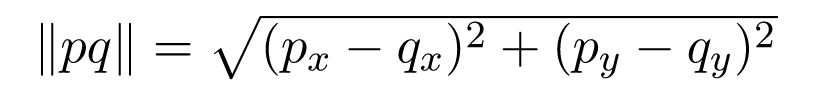
And lastly, we often find that naive approaches perform better for less number of data points than the optimized one. Optimized algorithm performs outstandingly for large number of data points. This problem is not an exception. The naive algorithm, where for every point we compute distance with all other points to compute closest pair, which is a O(n2) algorithm where n = total number of given points.
Implementation:
I have discussed all the implementation logic in details in the inline comments in the code below:Time Complexity of the Sweep Line Technique Based Approach: O(nlogn) where, n = total number of given points. Please follow the comments in the code where time complexities are explained. Add up all the explained time complexities and they would add up to O(nlogn).
Related Must-Read Topics:
- 1d Range Search
- Convex Hull
-
Dual Line Sweep
& Rectangles Union -
2D Intervals Union
& Skyline Problem - Overlapping 1D Intervals
- Merging Overlapping 1D Intervals
- Separating Overlapping 1D Intervals
