

Merging 2-D Intervals (Rectangles)
Get started
জয় শ্রী রাম
🕉In this chapter, we will learn how to compute the Union of overlapping rectangles in 2-D plane with all their base (lower horizontal boundary line) at the same y-coordinate first.
We will discuss the concept here by solving Skyline problem. We will see how we can effectively leverage Sweep Line technique to solve this kind of problems.
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance
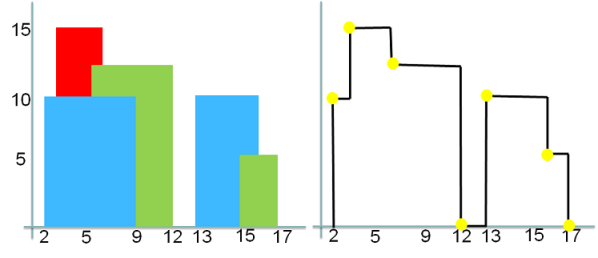
Now suppose you are given the x-coordinates and heights of all the buildings as shown on the left side of the image below. Our objective is to think through and come up with an algorithm to output the skyline formed by these buildings collectively, as shown on the right side of the image below.
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in the image below could be represented as: [[2,9,10], [3,6,15], [5,12,12], [13,16,10], [13,16,10], [15,17,5]] .
The output is a list of "key points" (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour. For instance, the output skyline for the image below should be represented as: [[2,10], [3,15], [6,12], [12,0], [13,10], [16,5], [17,0]]
In-depth Algorithm Discussion and Code Implementation:
Login to Access Content
Time Complexity:
If there are n number of buildings, then there are 2n vertical lines (start line and end line) we need to process.Sorting is O(2nlog2n) = O(nlogn).
Insertion and deletion from a heap are O(logn) operations. For 2n elements we have O(nlogn).
Overall time complexity = O(nlogn) + O(nlogn) = O(nlogn).