

Finding Bridges in a Connected Undirected Graph using Tarjan's Algorithm
Get started
জয় শ্রী রাম
🕉Prerequisites:
If you haven't already gone through the chapter on Articulation Points and watched the video, then please do so before reading this chapter as we will be using all the concepts introduced in Articulation Points chapter while discussing the algorithm to find Bridges in an undirected graph.Video Explanation of finding Bridges using Tarjan's Algorithm:
Let G = (V, E) be a connected, undirected graph. A bridge of G is an edge whose removal disconnects G.
In the diagram below all the bridges are the edges colored in red.
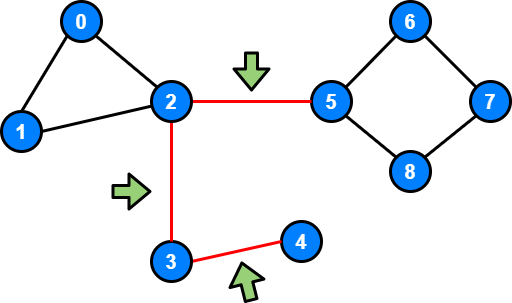
Two Important Observations:
-
If we apply the same concept of keeping track of
discovery time and earliest discovered node reachable and constructing
a DFS Spanning Tree
as discussed in the chapter
Articulation Points,
then for every bridges U-V
there is something interesting about the
earliest discovered node reachable from the subtree (subgraph with all the descendants of V) rooted at V
.
If edge U-V is a bridge and
U is discovered before V in the DFS, i.e, discoveryTime
of U is less than discoveryTime of V
then
the earliest discovered vertex reachable from the subgraph rooted at V will be a vertex with
discoveryTime GREATER than the discoveryTime of U.
And why is it so? It is because an edge U-V happens to be a bridge only when none of the vertices which were discovered before V in the DFS is reachable from the subtree (subgraph with all the descendants of V, in original given graph) rooted at vertex V in DFS Spanning Tree. Look at the connected undirected graph in the diagram below: the subgraph rooted at V which consists of V, W and X is NOT connected to any of vertices which were discovered before the root of this subgraph, and the root of this subgraph is V. To say in a different way, this subtree has no backedge that takes it to a vertex discovered before the root of this DFS subtree. So if the edge connecting the root (V) of this subgraph is to the root's parent (U) is removed the subgraph becomes disconnected from the rest of the graph.
So for all the descendents of V, the earliest discovered vertex happens to be V, and no other earlier discovered point. Which means the subgraph rooted at V is totally dependent on the back-edge U-V to be connected to the rest of the graph due to absence of any other backedge leading to a vertex discovered before discovering V.
So, in our Depth First Search (DFS) after we just backtracked from vertex V to vertex U if we see that the earliest discovered node reachable from V through its descendents and at most one back edge butnot using the back edge V-Uis LESS THAN OR EQUAL TO the discovery time of vertex U then the edge U-V is definitely not a Bridge.
The edge U-V is a Bridge when the earliest discovered node reachable from V through the descendants of V using at most one back edgebut not using the back edge V-Uis GREATER THAN the discovery time of vertex U.
NOTE: When I say subtree I refer to the subtree in the DFS Spanning Tree, but when I say subgraph I refer to the corresponding subgraph in the given original graph. The subtree and the corresponding subgraph will have same root, and have same nodes in it. For example, the subtree and its corresponding subgraph rooted at V: both of them have V, W and X as nodes.
Please click on the image below to enlarge it in a new tab. The whole algorithm we discussed above is depicted in the diagram below:
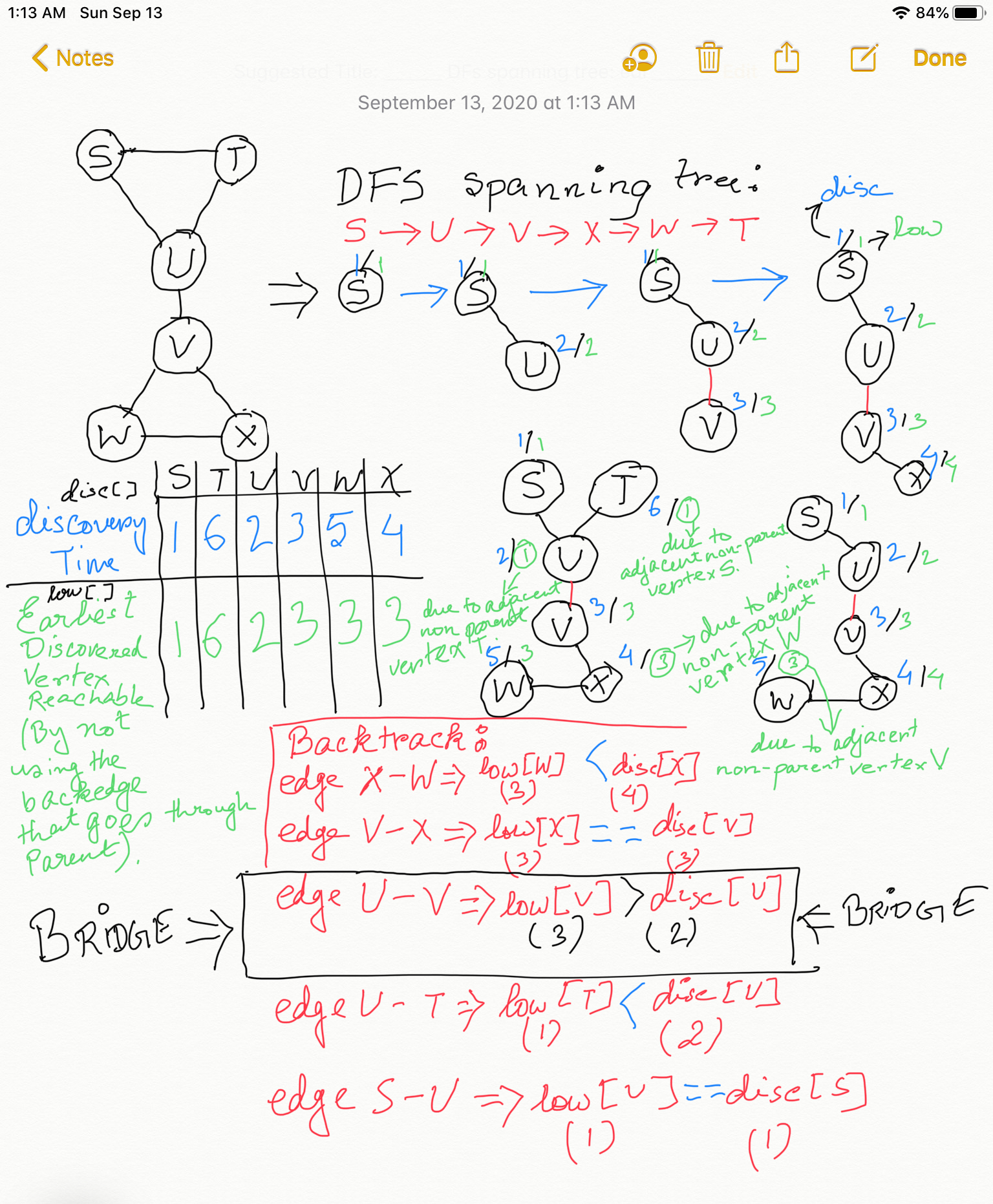
- Since we can do DFS from any vertex, we need to do a check to see if the logic discussed above ALWAYSholds true if any of the adjacent edge of the start vertex happens to be a bridge. A quick check by doing a DFS starting from either U and V in the graph in the diagram above shows that the logic discussed above in (1) applies as is for the start node of the DFS as well.
The code below implements the algorithm we just came up with:
Java code:
Login to Access Content
Python code:
Login to Access Content
Time Complexity:
The time complexity will be the time taken by the Depth First Search (DFS) : O(V + E), where V = total number of vertices in the connected undirected graph, and E = total number of edges in the graph. We are visiting all the edges and all the vertices while finding the bridges.Problem Solving:
Problem Statment: There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.A critical connection is a connection that, if removed, will make some server unable to reach some other server.
Return all critical connections in the network in any order.
Example:
2
/|
/ |
/ |
1 |
| \ |
| \|
| 0
|
3
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.
Solution:
This problem is about nothing but finding bridges in the given connected undirected graph. Take a look at the implementation below to see how we use the knowledge we gained in this chapter so far to solve real-world problems:Java code:
Login to Access Content
Login to Access Content
