

Tarjan's Algorithm for finding Strongly Connected Components in Directed Graph
Get started
জয় শ্রী রাম
🕉- After going through this chapter, definitely look at the chapters on Cycles: Often times problems that can be solved by using the concept of Strongly Connected Components can also be solved by leveraging the concept of Cycles. For any nodes 𝑎 and 𝑏, the node 𝑎 and 𝑏 belong to the same cycle if and only if 𝑎 and 𝑏 are strongly connected.
Prerequisite:
Video Explanation of finding Strongly Connected Components using Tarjan's Algorithm:
NOTE: Throughout the chapter I would be using the terms node and vertex interchangeably.
Please read the chapter Articulation Points before going through this chapter because all the fundamentals of Tarjan's Algorithm is discussed there. The algorithm of Finding Strongly Connected Components in a Directed Graph is built on top of the concept of discoveryTime and earliestDiscoveredNodeReachable introduced in Articulation Points.
What are Strong Connected Components in Directed Graph ?
Two vertices v and w are strongly connected if they are mutually reachable from each other. There is a directed path from v to w and a directed path from w to v. A directed graph is strongly connected if all of its vertices are strongly connected to each other. Al the 4 graphs in the diagram below are strongly connected directed graph.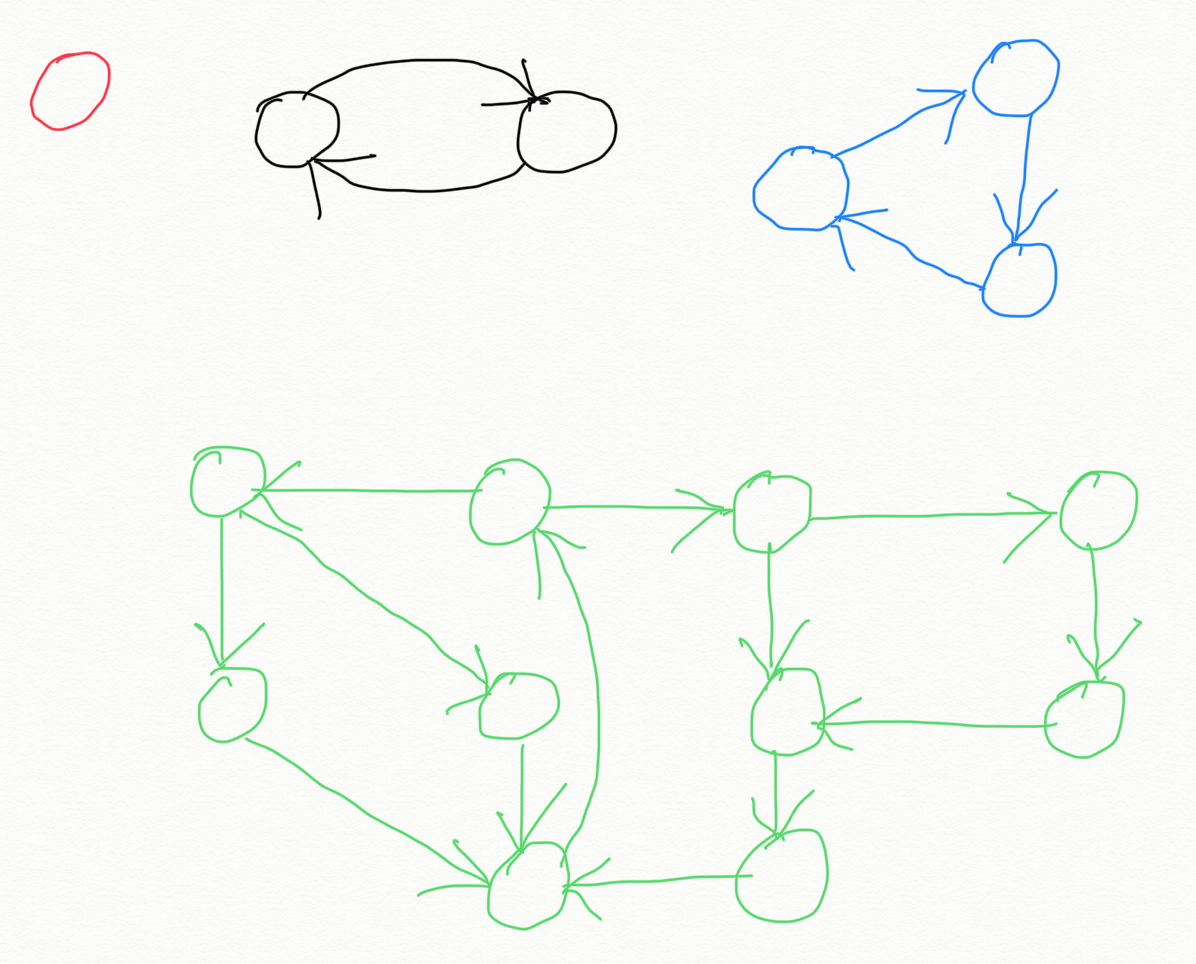
If a particular component in a directed graph is strongly connected then we call that component Strongly Connected Component or SCC. In an SCC all nodes are reachable from all other nodes.
If you think deeply you would observe two important things about strong connected components or SCCs :
-
Strongly Connected Components are basically cycles.
-
What is unique about SCC is that THERE IS NO WAY TO FIND A WAY THAT GOES OUT OF SCC AND THEN COMES BACK IN.
Look at all the diagrams in this chapter and get this statement clear to you. You should be able to convince yourself and this statement holds true for all SCCs. Because if you understand this simple concept it would be enough for you to figure out the algorithm to find SCCs yourself.
-
SCCs have no back-edge. Any outbound edge from any node in an SCC is always a Cross Edge leading to another SCC.
Look at the directed graphs and their Strongly Connected Components in the below two diagrams:
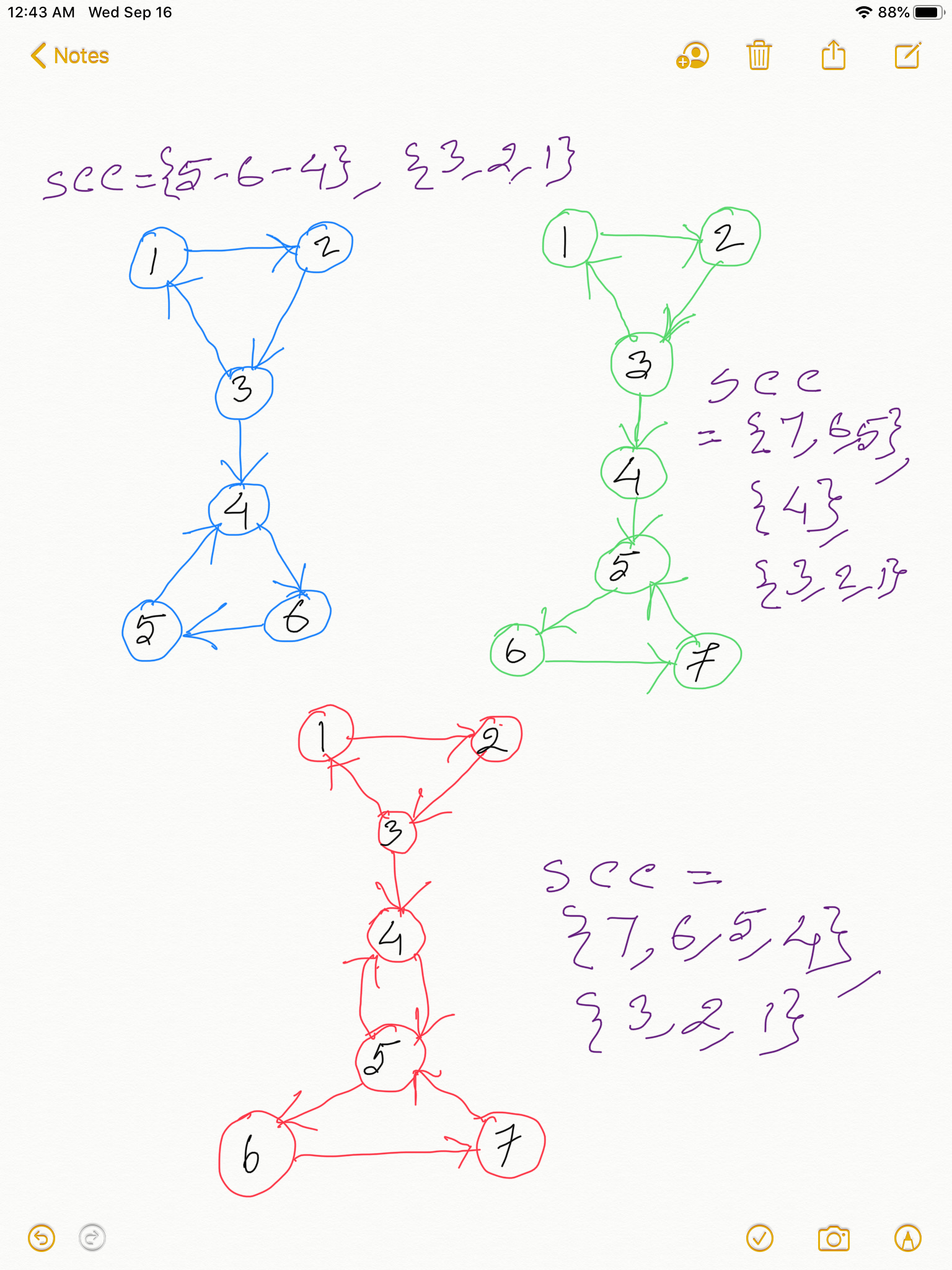
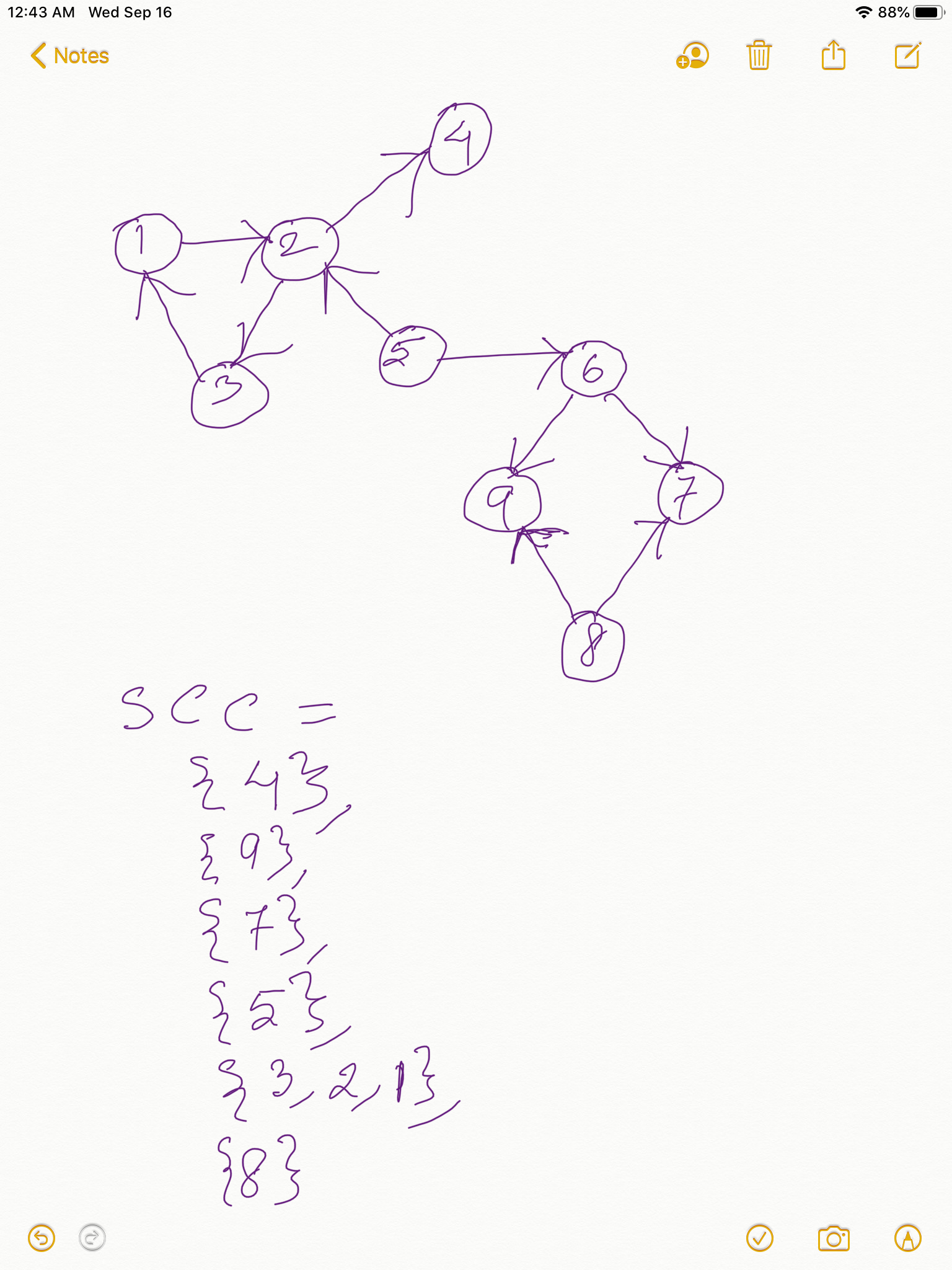
Take any Strongly Connected Component with more than one vertices in it from the above two diagrams. Just like in Finding Articulation Points here too if you construct a DFS spanning tree, since in any SCC THERE IS NO WAY TO FIND A WAY THAT GOES OUT OF SCC AND THEN COMES BACK IN, the earliestDiscoveredNodeReachable for all the vertices in an SCC will be the same as the discoveryTime of the root of the SCC in the DFS Spanning Tree, because SCCs are cyclic and the DFS root of the SCC is the earliest discovered node that is reachable from any node in the SCC. Take any SCC from the above two diagrams and this would hold true. Take a pause and please get this clear to you, because if you have understood this, congrats! you have already gotten the core of the algorithm.
So basically what we will do is, we will construct the DFS Spanning Tree in the same way as were doing for finding Articulation Points, and whenever we are done doing DFS on all of the adjacent vertex of a node (say, v) check: what is the lowestDiscoveredVertexReachable you got for the node v ?.
From above discussion we can summarize:
earliestDiscoveredVertexReachable[v] = discoveryTime[v],
then the vertex v is root of an SCC.
Cross Edges:
If you have observed, any node in an SCC can have an outbound edge going out of the SCC, but in all cases that outbound edge is either (1) a cross-edge, or (2) an edge that is leading to the next SCC. But the next SCC won't be part of the current SCC since according to our above discussing if a component is SCC there is no way to come back to it even if there is a way to get out.
Please note if an SCC has a cross-edge to other SCCs, we should discount those edges because cross edge always points a vertex which is already visited. This means the other SCC that the cross-edge is pointing to has already been processed. We would see in our code how we are identifying cross-edge. Draw two SCCs and connect them by one directed edge and you would be able to figure it out.
Quick Note:
- Back edges point from a node to one of its ancestors in the DFS tree.
- Forward edges point from a node to one of its descendants.
- Cross edges point from a node to a previously visited node that is neither an ancestor nor a descendant.
How would you keep track of all the vertices in a Strongly Connected Component in our code?
To track the subtree rooted at a specific node (say, vertex v), we can use a stack and keep pushing node while visiting. When we encounter the node v again while backtracking, pop all nodes from stack till you get head out of stack. This will make sure we pop only the nodes belonging to the SCC rooted at vertex v. Why ? Because if V is root of an SCC we will be visiting only the nodes belong to that SCC before we get back to vertex v while backtracking. Since SCC has no link to any other component we won't be visiting nodes outside of SCC before we backtrack to vertex v. This will become clearer when we look at the code.
To make sure, we don’t consider cross edges, when we reach a node which is already visited, we should process the visited node only if it is present in stack, else ignore the node.
Relationship with Topological Sort:
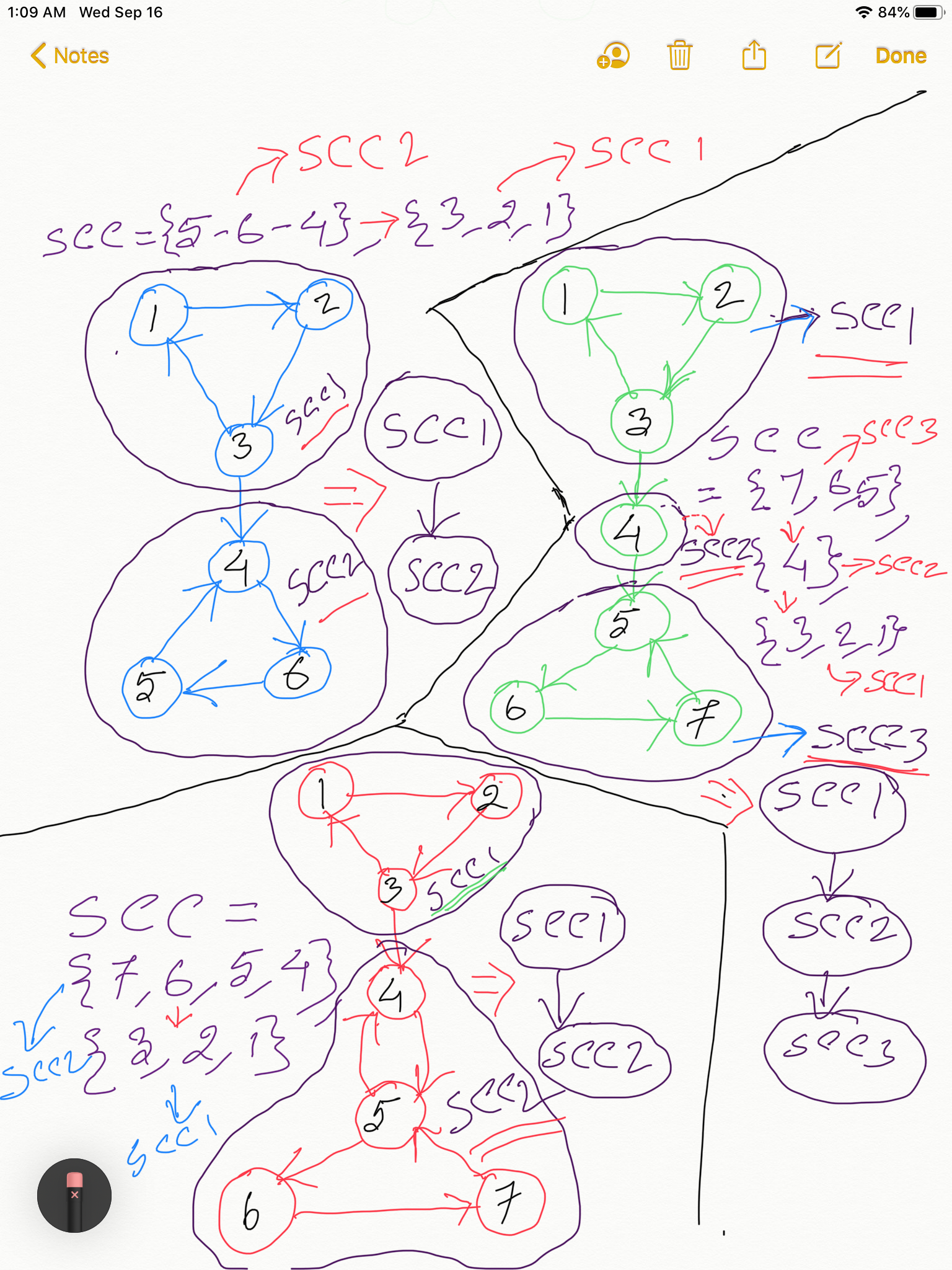
While there is nothing special about the order of the nodes within each strongly connected component, one useful property of the algorithm is that no strongly connected component will be identified before any of its successors. Therefore, the order in which the strongly connected components are identified constitutes a reverse topological sort of the DAG formed by the strongly connected components.This observation becomes quite intuitively if you recall the Topological Sort using DFS. There too we get the nodes in the opposite order of the topological order after the Depth First Search is done. Same thing here too since Tarjan's Algorithm uses DFS.
Course Scheduling demonstrates how we can leverage this observation to solve various problems.
The diagram below explains the above fact. Feel free to click on to open in a new tab:
 Donald Knuth described Tarjan's algorithm as one of his favorite implementations in the book "The Stanford GraphBase".
He also wrote:
"The data structures that he devised for this problem fit together in an amazingly beautiful way,
so that the quantities you need to look at while exploring a directed graph are always magically
at your fingertips. And his algorithm also does topological sorting as a byproduct.""
Donald Knuth described Tarjan's algorithm as one of his favorite implementations in the book "The Stanford GraphBase".
He also wrote:
"The data structures that he devised for this problem fit together in an amazingly beautiful way,
so that the quantities you need to look at while exploring a directed graph are always magically
at your fingertips. And his algorithm also does topological sorting as a byproduct.""
Pseudocode:
algorithm Tarjan :
input: graph G = (V, E)
output: set of strongly connected components (sets of vertices)
index := 0
S := empty stack
for each v in V do
if v.index is undefined then
strongconnect(v)
end if
end for
function strongconnect(v)
// Set the depth index for v to the smallest unused index
v.index := index
v.lowlink := index
index := index + 1
S.push(v)
v.onStack := true
// Consider successors of v
for each (v, w) in E do
if w.index is undefined then
// Successor w has not yet been visited; recurse on it
strongconnect(w)
v.lowlink := min(v.lowlink, w.lowlink)
else if w.onStack then
// Successor w is in stack S and hence in the current SCC
// If w is not on stack, then (v, w) is an edge pointing to an SCC already found and must be ignored
// Note: The next line may look odd - but is correct.
// It says w.index not w.lowlink; that is deliberate and from the original paper
v.lowlink := min(v.lowlink, w.index)
end if
end for
// If v is a root node, pop the stack and generate an SCC
if v.lowlink = v.index then
start a new strongly connected component
repeat
w := S.pop()
w.onStack := false
add w to current strongly connected component
while w ≠ v
output the current strongly connected component
end if
end function
Working Solution:
Java code:Login to Access Content
Python code:
Login to Access Content
